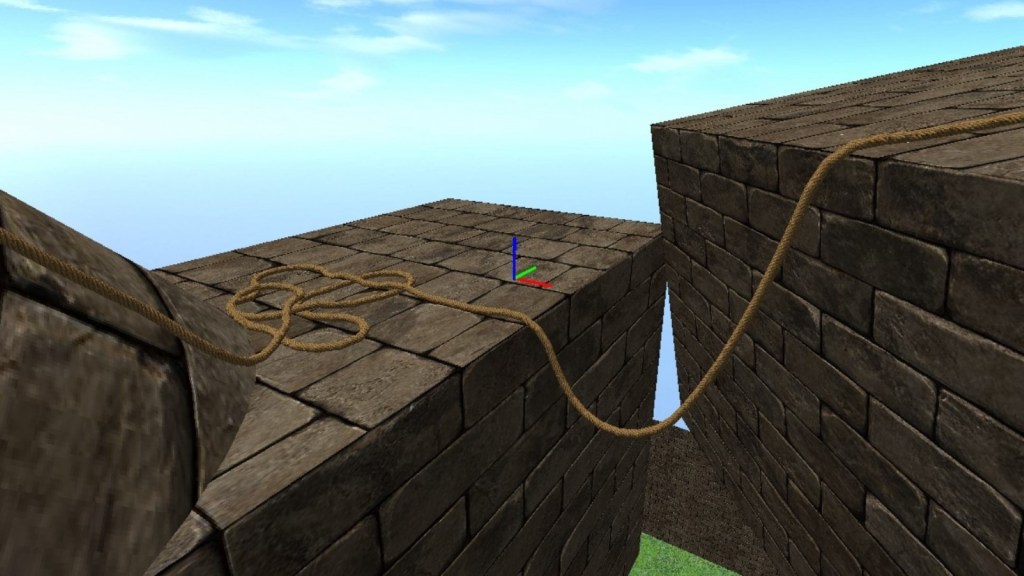
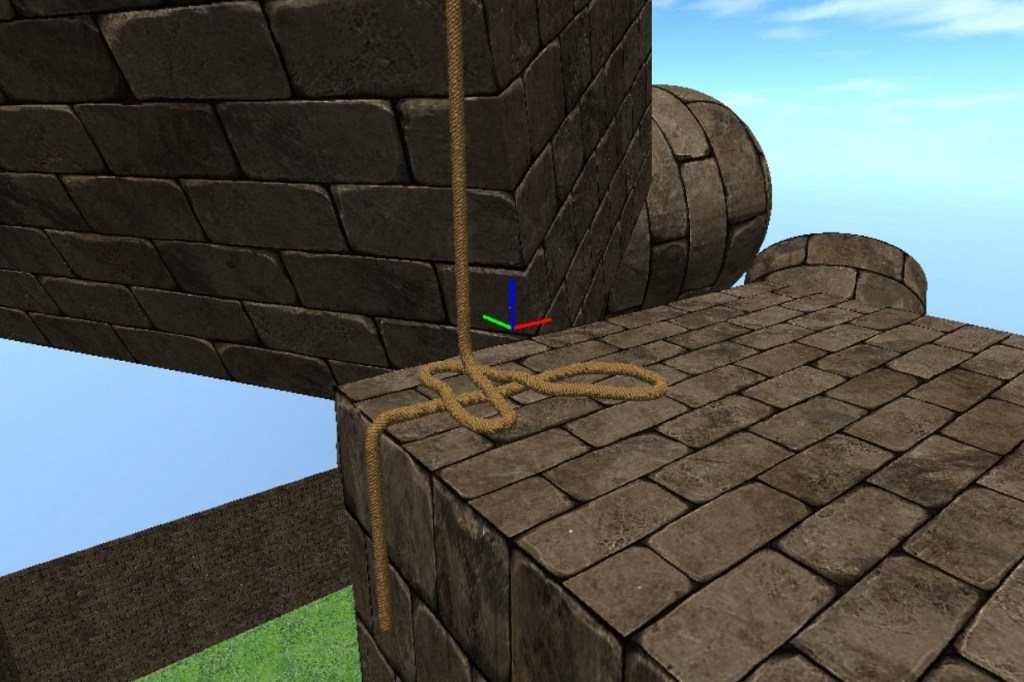
Rope Simulation

PBD is a simulation technique that disregards forces and instead directly manipulates positions through defined constraints and their projections. At the beginning of the simulation, constraints are created consisting of ‘n’ number of points, a function to satisfy the constraint, a stiffness parameter, and an equality type. From here, the solver runs every frame proposing new positions and then using a Gauss-Seidel iteration technique it then projects one constraint at a time sequentially. This constraint projection occurs based on a preset number of iterations depending on the performance and accuracy required. At the end of each frame, new positions are set and new velocities are calculated based on the current and proposed positions. The PBD solution for this project follows the same solver technique and only has constraints for distance, bending, and collisions.

This rope simulation has collision constraints that are generated for both sphere and capsule-based collisions against convex polygons such as AABBs, OBBs, cylinders, capsules, and spheres. Specifically, the sphere collisions provide for a faster collision solution when the density of points on the rope are greater than or equal to 1. But with a smaller density of points on the rope, the capsules provide a collision solution that has can handle collision without any unwanted visual artifacts. Beyond just objects in the scene, both collision techniques can handle self collisions on the rope itself.

To combat the performance issues that come from generating collision constraints in each substep and iteration of the solver, I implemented a bit-bucket spatial partitioning algorithm. This algorithm works by first splitting the world into 64 macro regions and then for each macro region I further split them into 64 micro regions. Each point on the rope, and collision object in the world has an associated uint64_t that represents the macro and micro regions. Once all bending and distance constraints have been projected, I then go through and find where each point/object intersects each of these macro and micro regions. Once the intersecting regions are found, the associated bits are marked with a 1 so when the collision constraints are being generated, a simple bitwise & can be used to perform early out collision checks on a macro and micro scale. This use of a bitwise & is severely faster than having to do distance squared checks to all the other points and collision objects in the scene.

The biggest challenge with this rope simulation is the performance of a rope in a level. Adding more points, constraints, solver iterations, or collision objects to a level only makes the performance speed slower. To combat this, I used DirectX 11 compute shaders to solve all constraints and perform all position and velocity updates in parallel on the GPU using a Jacobi solver. After the compute shaders simulate all the new positions, these points are sent to a geometry shader to build all the rendered vertices in parallel on the GPU.